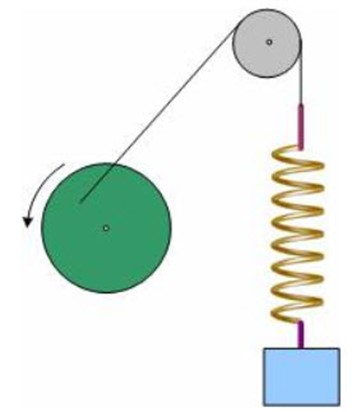
ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΤΑΛΑΝΤΩΣΗ
Τάδε έφη Διονύσης Μάργαρης:
Έστω ένα σώμα που εκτελεί εξαναγκασμένη ταλάντωση με την επίδραση μιας εξωτερικής δύναμης της μορφής F=F0ημ(ωt+φ0) και που η απομάκρυνσή του δίνεται από τη σχέση x=Αημωt. Για την ταχύτητα ταλάντωσης έχουμε:
υ= dx/dt = Αω·συνωt
όπου ω η γωνιακή συχνότητα της εξωτερικής δύναμης, δηλαδή η συχνότητα του διεγέρτη.
Για την ταλάντωση αυτή ισχύει ότι Umax=Κmax ?
Ας πάρουμε το λόγο:
Umαx/Κmax= ( ½ kΑ2)/( ½ mυmax2) = kΑ2/mΑ2ω2 = k/mω2 = mω02/mω2 = ω02/ω2 →
Umαx/Κmax= 4π2f02/4π2f12 = f02/f2. (1)
Όπου ω0 η γωνιακή ιδιοσυχνότητα του ταλαντωτή.
Ας πάρουμε τώρα την καμπύλη συντονισμού.
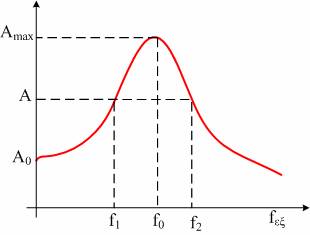

Διακρίνουμε τρεις περιπτώσεις.
Α) Αν fδιεγ = f1 όπου η συχνότητα f1 είναι μικρότερη από την ιδιοσυχνότητα f0, η σχέση (1) δίνει:
Umαx/Κmax= f02/f2 > 1 ή Umax> Κmax.
Β) Αν fδιεγ = f2 όπου η συχνότητα f2 είναι μεγαλύτερη από την ιδιοσυχνότητα f0, η σχέση (1) δίνει:
Umαx/Κmax= f02/f2 < 1 ή Umax < Κmax.
Γ) Αν fδιεγ = f0 όπου f0 ιδιοσυχνότητα, η σχέση (1) δίνει:
Umαx/Κmax= f02/f2 = 1 ή Umax= Κmax.
Συμπέρασμα:
Μόνο στην περίπτωση που η συχνότητα του διεγέρτη είναι ίση με την ιδιοσυχνότητα του συστήματος, η μέγιστη δυναμική είναι ίση με την μέγιστη κινητική ενέργεια ταλάντωσης.
Και ερχόμαστε τώρα στο θέμα του ΣΥΝΤΟΝΙΣΜΟΥ. Τι ονομάζουμε συντονισμό; Την περίπτωση που το πλάτος ή την περίπτωση που η υmaxείναι μέγιστη; Θα πείτε υπάρχει διαφορά;
Η απάντηση είναι ΝΑΙ. Ας πάρουμε τις γραφικές παραστάσεις του πλάτους της απομάκρυνσης και του πλάτους της ταχύτητας σε συνάρτηση με την συχνότητα του διεγέρτη.
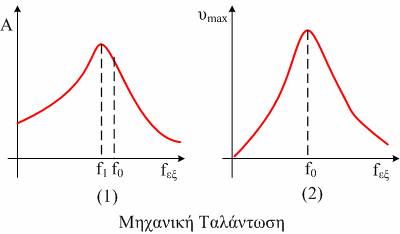

Το πλάτος (της απομάκρυνσης) γίνεται μέγιστο για μια συχνότητα f1 λίγο μικρότερη από την ιδιοσυχνότητα f0, ενώ το πλάτος της ταχύτητας γίνεται μέγιστο για συχνότητα ακριβώς ίση με την ιδιοσυχνότητα f0. (προσέξτε λίγο και την διαφορά των δύο γραφικών παραστάσεων για πολύ μικρές τιμές της fεξ.
---------------------♦♦♦♦♦♦♦♦♦♦♦♦♦---------------------------
ΓΙΑ ΝΑ ΚΑΤΑΛΑΒΟΥΜΕ ΤΟ ΣΥΝΤΟΝΙΣΜΟ ΑΣ ΔΟΥΜΕ ΤΟ VIDEO...!
---------------------♦♦♦♦♦♦♦♦♦♦♦♦♦---------------------------